Sign in Subscribe

Alveolar Gas Equation

Last updated on 
Alveolar Gas Equation
Photo by Rohit Tandon / Unsplash

Take home messages

  • Try to understand the alveolar gas equation, and it'll make much more sense when you come to exam time and have to use it to answer questions
  • The equation lets us estimate the amount of oxygen in the alveoli, based on how much is being inhaled, and how much is being consumed by the body
  • It has lots of assumptions that you need to be able to recite

If you just want to memorise it - here it is

But if you want to understand it, then read on.

What is point of the alveolar gas equation?

I mean, we're anaesthetists, so we love a bit of maths for maths' sake, but most of the time there is a good reason why we crunch the numbers and go to the trouble of deriving equations in our spare time.

If we know the partial pressure of oxygen in the alveolus, we can figure out how efficiently the lungs are working, because we can compare the amount of oxygen in the alveolus and the blood to the amount that we're giving the patient.

💡
The A-a gradient - comparing the alveolar and arterial partial pressures of oxygen - is used in determining the severity of V/Q mismatching.

However it’s very difficult to actually measure the partial pressure of oxygen inside an individual alveolus - let alone all of them - so instead we use the alveolar gas equation is used to estimate it, using values that are much easier to directly measure.

The things we can measure

  • The partial pressure of oxygen in an arterial blood gas sample - PaO2
  • The fraction, or percentage, of oxygen in the inspired air - FiO2
  • The partial pressure of carbon dioxide in the blood - PaCO2
  • Atmospheric pressure - Patm
  • The saturated vapour pressure of water at 37°C - PH2O*
  • How much oxygen is needed for each molecule of CO2 released by metabolism - Respiratory Quotient (R)

*We need to know this is because water vapour has its own partial pressure, and will therefore contribute to the overall pressure of the inspired gas mixture as the gas is humidified by the upper airways. 

It is usually around 47 mmHg or 6.3 kPa.

What the alveolar gas equation actually estimates:

This post aims to explain how we use these measurable variables to make the following equation:

Amount of oxygen in alveolus = oxygen breathed in - oxygen removed*

*(either into the blood or exhaled)

We also need, as is customary with modelling the infinitely complex human body using maths, to make some general assumptions about how the gases - and the body - behave.

What assumptions are required for the alveolar gas equation?

  • The patient is at steady state, so there is no accumulation or loss of CO2 or oxygen
  • All gases obey Dalton’s law of partial pressures*
  • CO2 diffuses across the alveolar capillary membrane essentially instantaneously - This is important because it means we can use PACO2 (hard to measure) and PaCO2 (easy to measure) interchangeably
  • There is no rebreathing of CO2, so FiCO2 is zero
  • FiO2 is warmed and maximally saturated with water by the upper respiratory tract (we need this assumption to calculate the PH2O)

*Dalton's law asserts that each gas in a mixture exerts its own partial pressure, and these all add up to give the overall pressure of the mixture as a whole.

For example a 50:50 mixture of nitrogen and oxygen at atmospheric pressure of approx 100 kPa would be 50 kPa O2 and 50 kPa N2

Deep breath.

Here we go.

Carbon Dioxide comes from the cells.

CO2 is produced on average at around 200ml per minute, whereupon it promptly enters the bloodstream and is carted off to the lungs.

If our steady state assumption applies, then we must therefore be exhaling 200ml per minute of CO2 as well.

Given it is very very difficult to measure the alveolar partial pressure of CO2 (PACO2) and vastly easier to measure the arterial partial pressure of CO2 instead (PaCO2), it would be nice if we could just use the latter term instead.

Fortunately, as CO2 diffuses so blindingly quickly across the alveolar capillary membrane, we make the assumption that PACO2 = PaCO2.

How convenient.

We also assume that there is no rebreathing of CO2, so all of it is exhaled.

Therefore the rate at which CO2 is produced (VCO2) must be equal to the rate at which it is exhaled.

Rate of exhalation = Fraction exhaled CO2 (FACO2) x Minute ventilation (Va)

This is how we get to this point:

VCO2 = FACO2 x Va

Oxygen has one way in, and two ways out.

Oxygen is inhaled from the atmosphere, and the amount that is inhaled per minute depends on three variables:

  • Atmospheric pressure (Patm)
  • The percentage of that pressure that is due to oxygen (FiO2)
  • Minute ventilation (Va)
💡
This is why you hyperventilate at altitude - the percentage of oxygen is still 21%, however atmospheric pressure has dropped, so you have to increase your minute ventilation to avoid hypoxia

Easy.

But wait.

Some of this oxygen is then exhaled again, which we need to account for:

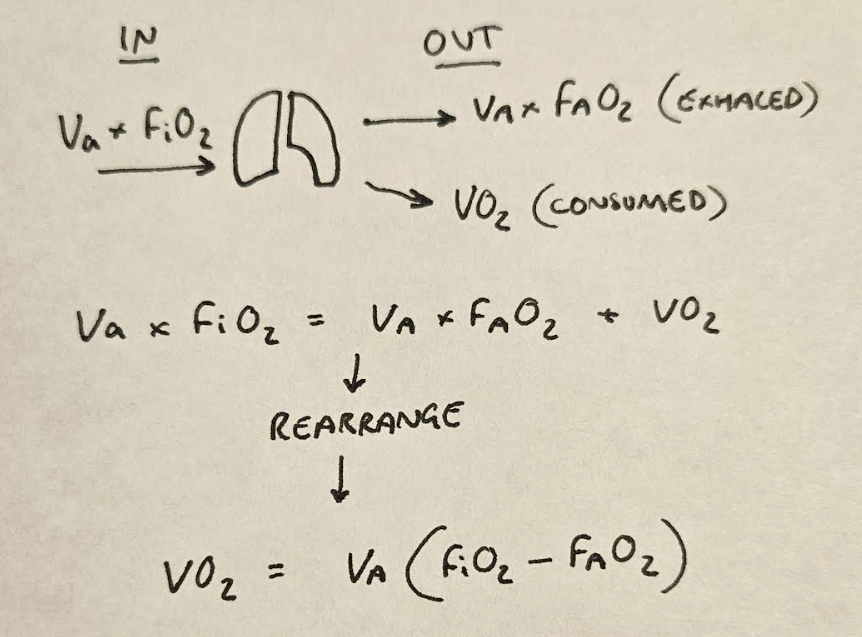
Oxygen consumption is approximately 250ml/min in an average adult

This is how we get to this point:

VO2 = Va x (FiO2 - FAO2)

Quick breather

We have now have two separate equations, telling us two useful bits of information.

  • The rate of CO2 production:
VCO2 = FACO2 x Va
  • and the rate of oxygen consumption:
VO2 = Va x (FiO2 - FAO2)

If we can link the two, then we can figure out how much oxygen we're expecting to remove from the alveolus - both exhaled and switched for CO2 as a result of metabolism.

So how do we link them?

What on earth is 'R'?

We know that in aerobic metabolism, oxygen is consumed, and carbon dioxide produced.

The respiratory quotient is simply the ratio of carbon dioxide production to oxygen consumption.

R = VCO2/VO2

What is the value of R?

  • Carbohydrate molecules have oxygen already built in, meaning less extra oxygen is needed to produce the same amount of CO2
  • Pure carbohydrate metabolism releases one carbon dioxide molecule for each oxygen molecule consumed, so the respiratory quotient (R) = 1
  • Fat molecules have vastly fewer oxygen molecules, and therefore consumes a lot more oxygen for each CO2 molecule produced, so the R = 0.7
  • It is assumed that for a normal individual, the R is usually around 0.8 for the purposes of this equation

This is enormously convenient to know, because we already have the equations for VCO2 and VO2, so being able to stitch them together using R is very helpful indeed.

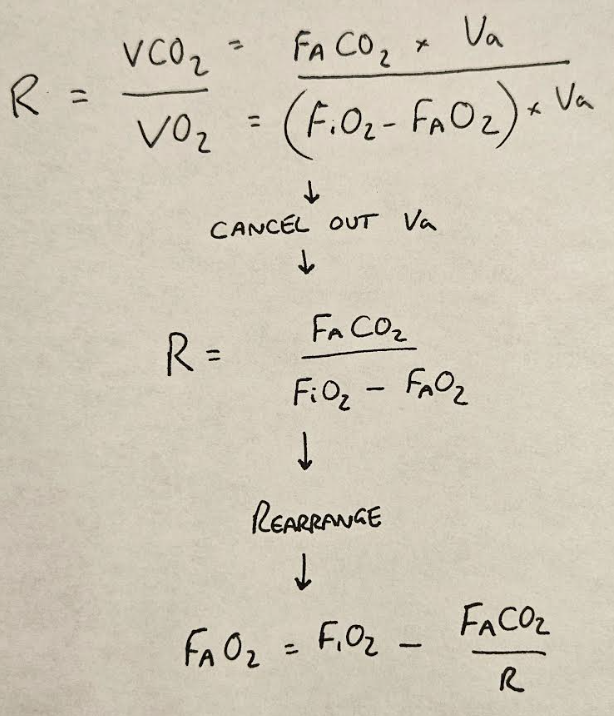
We then simply switch the F's for P's, as we assume Dalton's law to be true, and PACO2 for PaCO2 as we mentioned earlier, and we end up with:

PAO2 = PiO2 - PaCO2/R

This is the alveolar gas equation in its simplest form

And it tells us that the amount of oxygen left in the alveolus is equal to the amount breathed in, minus the amount swapped for CO2 or exhaled.

If you wrote this in an exam, you'd likely get most of the marks. The rest is frankly lots of nuance.

Why does warming and humidification matter?

As we mentioned earlier, the inhaled gas mixture has a pressure (Patm) and a concentration or fraction of inspired oxygen (FiO2)

Therefore we can calculate the first term PiO2 - the partial pressure of inspired oxygen - as:

PiO2 = FiO2 x Patm
21% x 101.3kPa = 21.3kPa O2 reaching the lungs

But there's an issue.

As room air passes through the nose and pharynx, it is warmed and has water vapour added, to protect the tracheal mucosa and prevent excessive heat loss during breathing.

While this is all well and good for our respiratory tract, it somewhat confuses our equation, because our inspired gas mixture now has another component - the water vapour.

As per Dalton's law, this water vapour contributes its own partial pressure, which - given we're assuming the gas has been maximally saturated by the upper respiratory tract - is the saturated vapour pressure at 37°C.

💡
We call this term PH2O and we assume it to be around 6.3kPa

Because this water vapour cannot hold any oxygen, it reduces the overall inspired concentration of oxygen, which we have to account for in our equation.

This is why we have the FiO2 x (Patm-PH2O) term.

21% x (101.3 - 6.3) = 19.95 kPa O2 reaching the lungs

It's a small difference, but it matters.

The equation therefore looks like this:

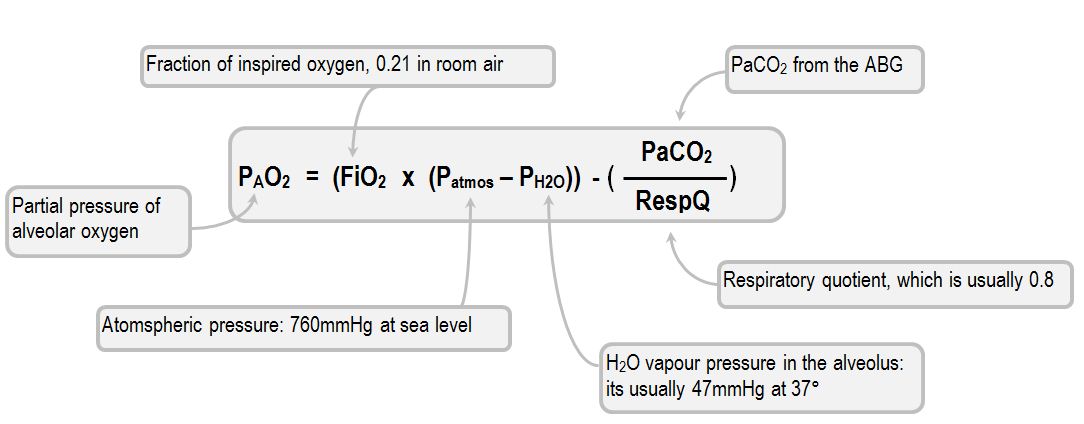
PAO2 = [FIO2 × (Patm − PH2O)] − (PACO2 /R)

Which is what we saw at the beginning of this post.

Well done.

You made it.

Worked example

Let's use the equation for a normal person standing at sea level, to see how it works.

Assuming:

  • 21% oxygen
  • Standard atmospheric pressure of 101.3kPa
  • Normal PACO2 of 5 kPa
  • R = 0.8
PAO2 = FiO2(Patm – PH2O) – PACO2/R
PAO2 = 0.21(101.3 – 6.3) – 5/0.8
PAO2 = 19.95 – 6.25
PAO2 = 13.7 kPa

This fits with our clinical observations that a 'normal' PAO2 in a healthy person is around 13kPa at rest.

Hooray, it works.

How is the alveolar gas equation affected by altitude?

The FiO2 remains constant at 21% as altitude increases, however atmospheric pressure decreases. Therefore the term FiO2(Patm-PH2O) will decrease as well, resulting in reduced PAO2.

What will be the PaO2 of a person in an aircraft with a cabin pressure of 80kPa?

Assuming 21% oxygen, a normal PACO2 of 5 kPa, and R = 0.8

  • PAO2 = FiO2(Patm – PH2O) – PACO2
  • PAO2 = 0.21(80 – 6.3) – 5/0.8
  • PAO2 = 15.5 – 6.25
  • PAO2 = 9.25 kPa

This is why aircraft cabins are pressurised, and in the event of cabin decompression, those ominous oxygen masks flop down from the ceiling. 

A Common SOE question

What does the alveolar gas equation tell you about the relationship between inspired oxygen concentration and PAO2?

This question is testing your understanding of how the terms in the equation relate to one another.

The equation is PAO2 = PiO2 - PaCO2/R

If PAO2 is the y variable, and PiO2 the x variable, then this is an equation in the form

y = mx + c

This is a linear graph and therefore shows the relationship between the two is linear

Therefore increasing the inspired oxygen concentration will increase the PAO2 in a linear fashion, as shown in the graph below.

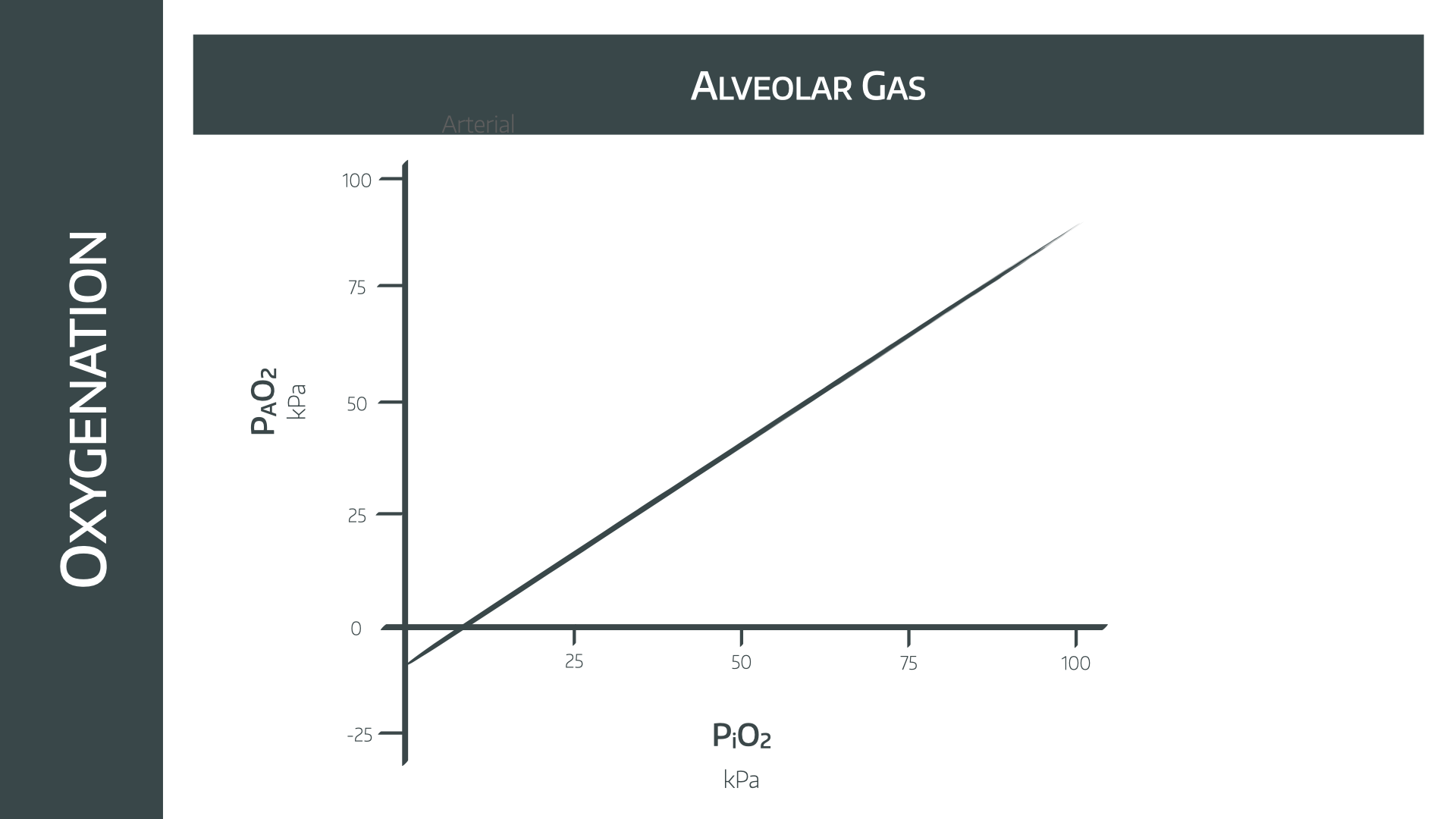
Alveolar Gas.002.png

The weird bit on the left where the PAO2 is calculated as being negative is accounted for by our first assumption - the patient is in a steady state.

Clearly being dangerously hypoxic to the point of having a negative PAO2 is hardly 'steady' and so we ignore that bit.

Only if you're really keen

You do not need to know this bit for the exam, or ever really.

If you think about the fact that we breathe out about 200ml of CO2, but consume around 250ml O2 per minute, you'll realise there is a 50ml per minute discrepancy.

If we assume the lungs aren't collapsing and their volume remains the same, then this reducing volume must cause a decrease in pressure within the lungs.

Assuming the airway is open, this decrease in pressure will 'suck' more air down the trachea, and therefore a tiny bit of extra oxygen will enter the alveolus.

This gives us this weird extra term:

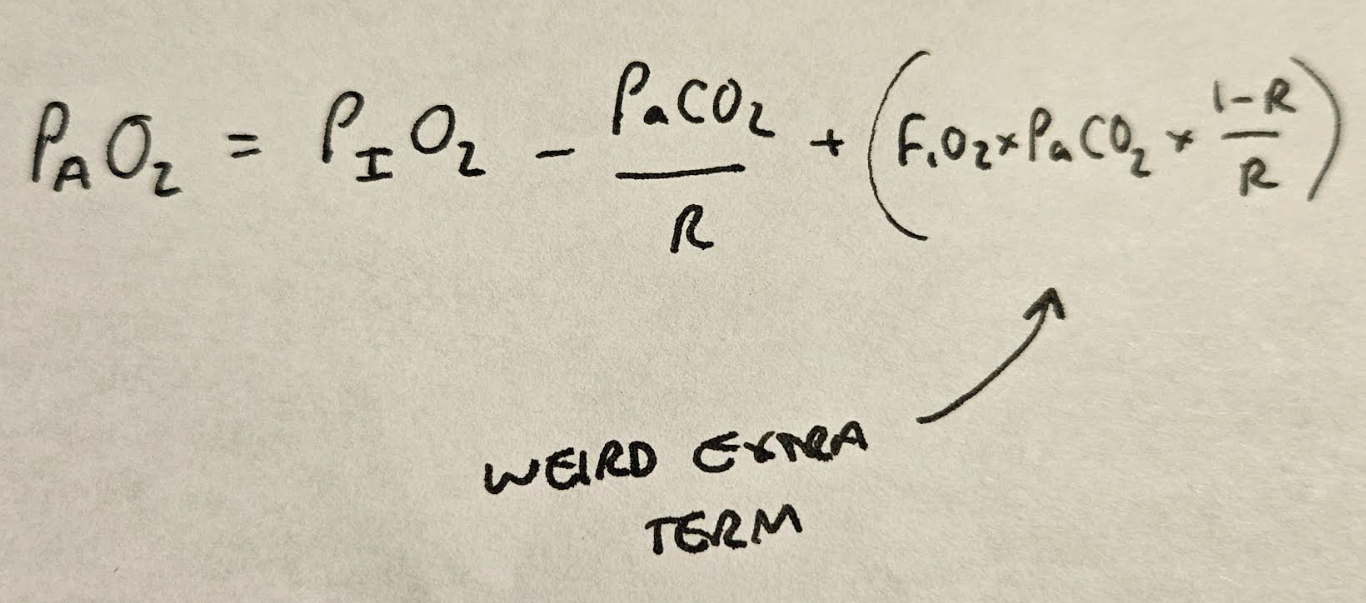
Which has negligible clinical relevance as the extra oxygen in the alveolus as a result is absolutely tiny.

Please do not waste time learning this for the exam - it won't gain you extra marks!

If you're interested in how that extra term is derived, read this article

A TikTok we made

@anaestheasier

The Alveolar Gas Equation full article at anaestheasier.com

♬ original sound - Anaestheasier

Useful Tweets

References and Further Reading

alveolar gas equation
Abstract. The alveolar gas equation (AGE) is well known and relates the alveolar concentration of oxygen Fao2 (or equivalently partial pressure Pao2) to three v
OUP AcademicSteven Cruickshank, BA MB BS FRCA
The alveolar gas equation
This equation describes the concentration of gases in the alveolus, and thus allows us to make educated guesses as to the effectiveness of gas exchange. One can use this to calculate the tension-based indices of oxygenation, such as A-a gradient or the a/A ratio (which is expressed as a percentage).…
Deranged PhysiologyAlex Yartsev
A-a O₂ Gradient - MDCalc
The A-a O2 Gradient assesses for degree of shunting and V/Q mismatch.
MDCalcDr. H. Fred Helmholz

Primary FRCA Toolkit

Members receive 60% discount off the FRCA Primary Toolkit. If you have previously purchased a toolkit at full price, please email anaestheasier@gmail.com for a retrospective discount.

Free version available here

Discount is applied as 6 months free membership - please don't hesitate to email Anaestheasier@gmail.com if you have any questions!

Members Area

Test your knowledge!