Force and Pressure

Take home messages

• You need to understand the basic physics underpinning the equipment we use and the physiology we abuse
• Force = mass x acceleration
• Pressure = force / area

You can figure most answers out using just these two equations.

Don't force it

As with all things in exams, if you can understand something, it's easier than trying to just remember it on exam day, so we'll build it up from the absolute basics, and try to make it make sense.

A force is an influence that will act to change the state of rest, or state of motion, of an object, and usually comes about by interaction with another object.

Force is measured in newtons, where one newton is the force required to accelerate a 1kg object at 1 metre per second per second.

• N = kg x m/s²

Gravity is a force, and will cause any object to accelerate at 9.81 m/s². This means for a 1 kg mass, the force applied by gravity is 9.81 N.

Weight therefore is defined as the force exerted by an object as a result of gravity's influence.

So basically to get from kg to N just times it by ten-ish.

Pressure

Wear stiletto heels to a garden party and you'll find yourself sinking into the turf, because your body weight is applied over a tiny area.

In fact even an elephant generates less pressure on the ground than a human being in heels, because the force is spread out over a much larger area.

An elephant wearing large snow shoes would generate even less pressure.

By this logic we can get our elephant to float if we just find some shoes big enough...

Let's move on.

The SI unit of pressure is the pascal (Pa) which is equivalent to 1 N per square metre.

• 102g of weight over a whole square metre is a miniscule amount of pressure
• 1 mmHg is 133 Pa.
• 1 cmH₂O is 98 Pa.
• So we usually use kilopascals (kPa) instead
• 1 bar = 100 kPa = approximate atmospheric pressure at sea level
• Atmospheric pressure depends on altitude and weather (affects the density of the air)

The pressure in your oxygen cylinder is 137 bar, or 13 700 kPa, which is rather a lot.

The interplay between pressure and force is neatly demonstrated by syringes and pressure reducing valves.

Pressure reducing valves

If you want to reduce the pressure of a fluid, then you need to manipulate the area over which it is applying a force.

By making two columns of fluid exert the same force against each other, but on different size areas, they will therefore be at different pressures, as demonstrated in our video here.

Endotracheal cuffs

Older fashioned tubes had low volume, high pressure cuffs, which would apply far more force to the tracheal mucosa, providing a better seal but risking more damage.

Newer cuffs tend to have higher volume, lower pressure cuffs, which compensate for the less forceful seal by having more surface area of the trachea covered.

The result is a decent seal and much less tracheal necrosis.

Pressure in liquids

If you have a column of liquid, the pressure at the bottom of the column depends on the height of the column, and not the width.

You'll notice that some of the units involve a height and a fluid (mmHg, cmH2O) so theoretically you could measure pressure with whatever you like:

• Kilometers of orange squash
• Yards of bleach
• Lightyears of vodka

All would be valid, albeit useless, measures of pressure.

It may seem counterintuitive that a very wide column of water and a very narrow one could be exerting the same pressure if they're the same height, but thanks to some simple maths, they do.

This means that for very 10 metres you descend in the ocean, the pressure increases by another atmosphere.

Mercury is 13.6 times more dense than water, so instead of ten metres, you only need 760 mm or 76 cm of mercury to generate an atmosphere of pressure.

Arterial lines

This is why you need to make sure your arterial line transducer is at the correct height (i.e. level with the right atrium).

If the transducer is lower than the heart, then the column of fluid in the tubing will exert an additional pressure on the transducer membrane, giving a falsely high reading.

If the transducer is raised up in the air, the column of fluid exerts a downwards and therefore negative pressure on the membrane, giving a falsely low reading.

Surface tension

If you have a really narrow column of fluid, you can get to the point where surface tension starts to interfere with your physics equations.

Surface tension refers to the intermolecular forces of attraction on the surface of a liquid that make it behave almost as if it has a 'skin', and it's this tension that gives fluid a meniscus.

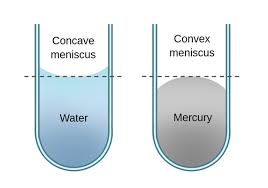
Depending on how the fluid interacts with the walls of the container, it can have a concave, convex or flat meniscus.

You can see this in action when the paediatrician takes an impossibly small blood sample from a baby's toe.

LaPlace's law

Laplace’s law links wall tension with pressure and radius in things containing fluid or gas.

These things are usually either cylindrical or spherical in shape, such as a blood vessel or alveolus.

As the thing distends, for any given pressure inside it, the tension in the wall will increase if the radius is bigger.

• This is why bigger aneurysms are more likely to rupture
• It's also how the reservoir bag protects your patient's lungs when you forget to open the APL valve - it distends more and more easily, reducing the pressure in the breathing system until you spot the enormous green ball on the floor and open the valve
• Dilated ventricles have to contract harder to generate the same pressure, hence the myocardial oxygen demand goes up

Conversely for a smaller radius, the pressure required to keep it open is higher (if surface tension is constant) hence smaller alveoli are at greater risk of collapsing without surfactant to reduce the surface tension.

For a cylinder:

For a sphere:

The way we remember this is that a sphere has 'roundness' in two directions where a cylinder only has one.

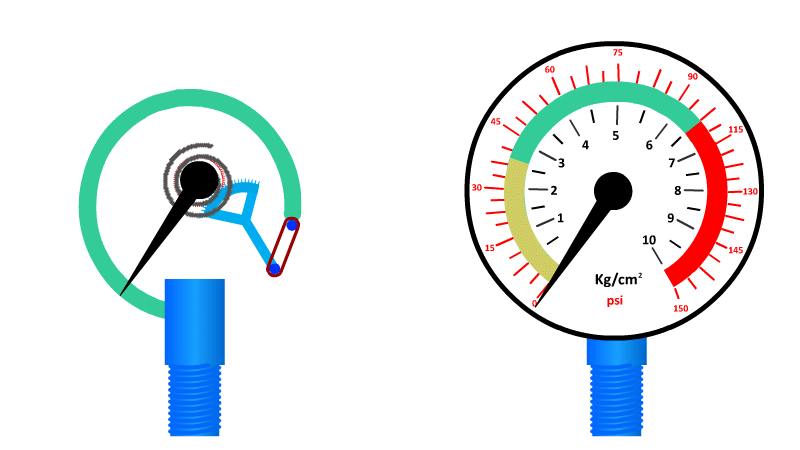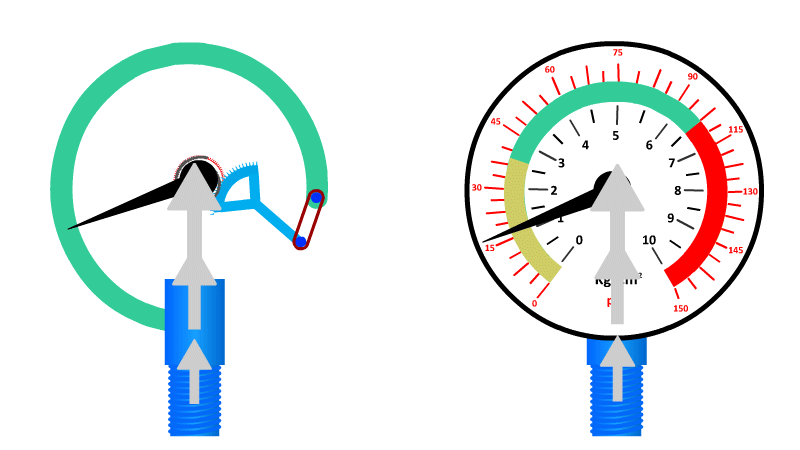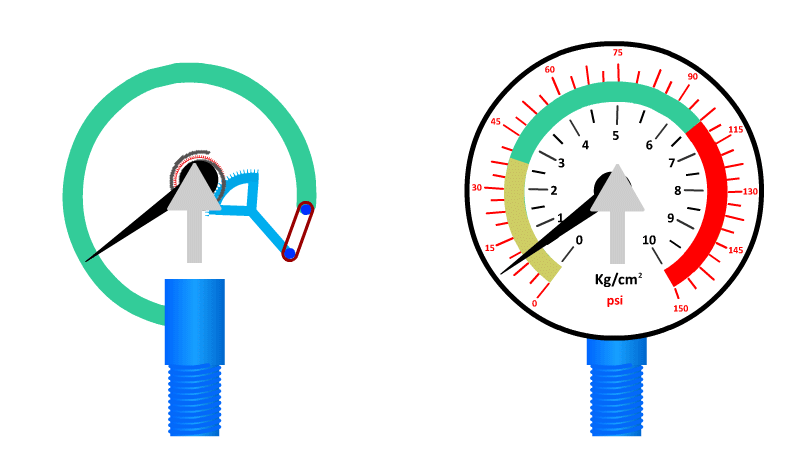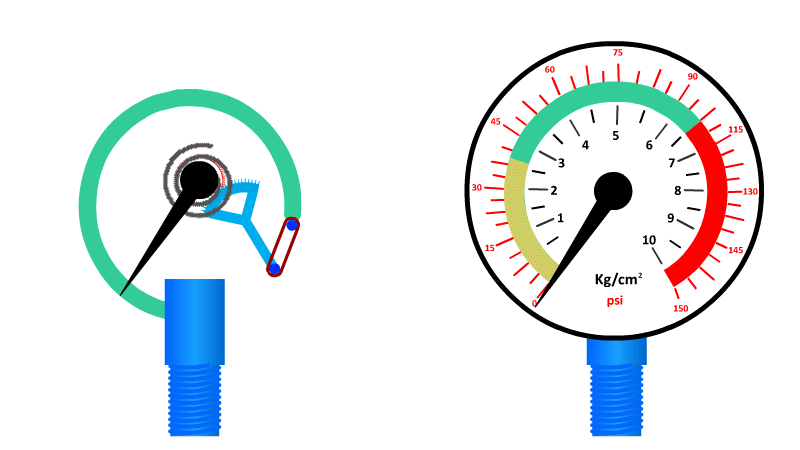
The Bourdon Gauge

More classic exam fodder.

Also called an aneroid from the Greek a-neros meaning without liquid, this gauge uses a spring and a coiled tube of air attached to a dial.

As pressure is applied to the tube of air, it straightens out and pushes the dial around to a pre-calibrated number. When the pressure is released the spring returns it to zero.

Here's our video on pressure in liquids

Here's all the equations you need to know for the primary FRCA exam

Equations

We’re building a list of all the equations we think you need for the FRCA exams. If there are any missing, let us know and we’ll add them! Pharmacokinetics and pharmacology Plasma concentration * Concentration = Dose/Volume of distribution * Loading dose = volume of distribution x desired concentration * Infusion rate = desired concentration

AnaestheasierAnaestheasier ltd.

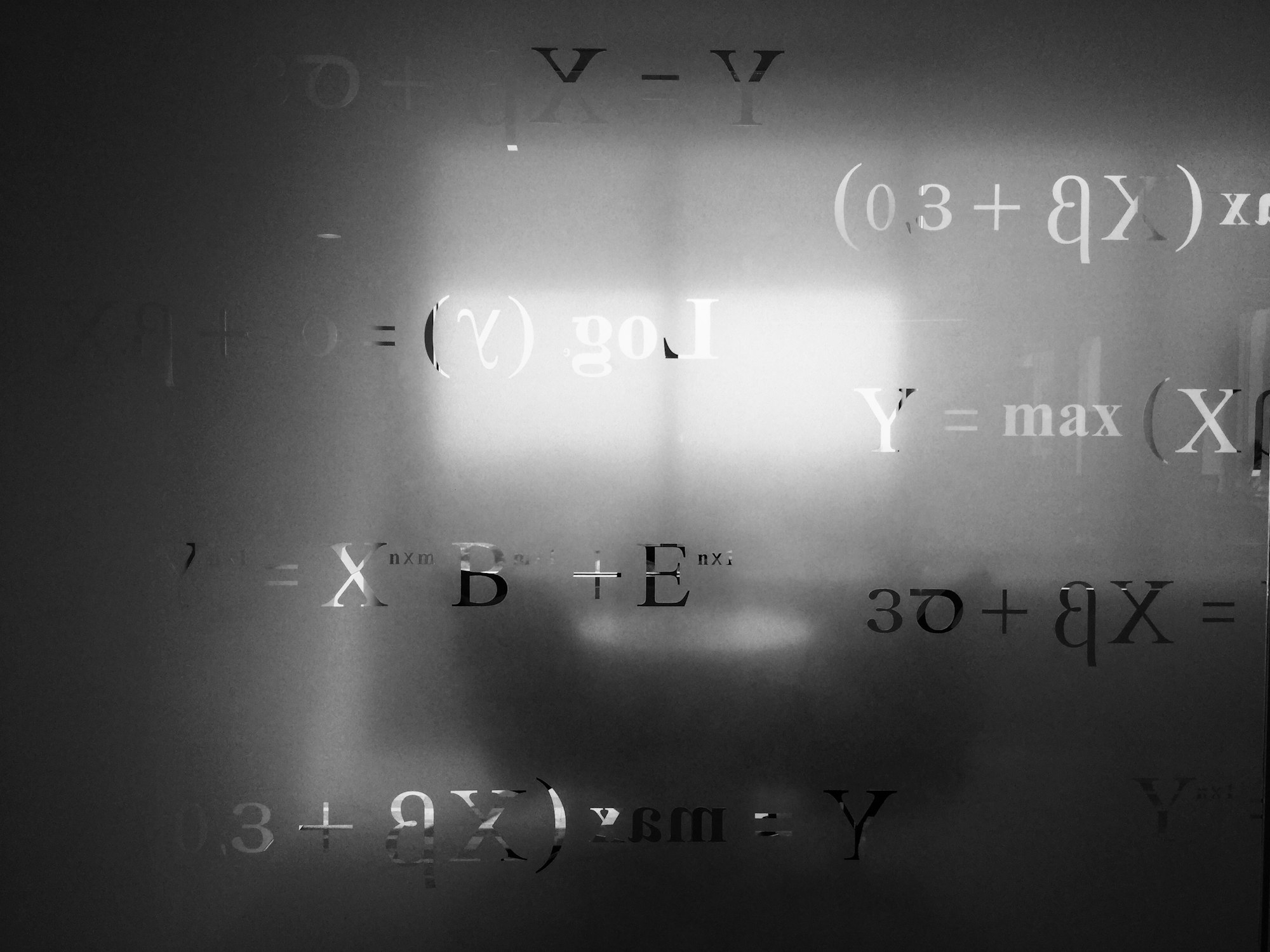
Primary FRCA Toolkit

Members receive 60% discount off the FRCA Primary Toolkit in the form of free membership.

If you have previously purchased a toolkit at full price, please email anaestheasier@gmail.com for a retrospective discount.

Discount is applied as 6 months free membership - please don't hesitate to email Anaestheasier@gmail.com if you have any questions!

Just a quick reminder that all information posted on Anaestheasier.com is for educational purposes only, and it does not constitute medical or clinical advice.